We want to determine the equation in point slope form for the line that is perpendicular to the given line and passing through the point (5.6) .
The equation and the point is;
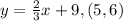
We know that for two lines to be perpendicular, the product of their slopes should be -1.
Therefore, the slope of the perpendicular should be;
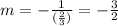
The second condition is that the line must pass through the point (5,6) , to do thid, we write the equation of the line in point slope form which is;
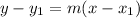
Inserting all values, we have,
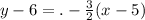
That is the final answer.