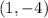The Vertex form of a Quadratic equation is:
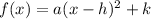
Where the vertex of the parabola is:
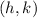
Given the following Quadratic equation:
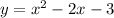
You can write in Vertex form by completing the square. The steps are:
1. You need divide the coefficient of the x-term by 2, square it and add it to both sides of the equation. Notice that:
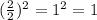
Then:

2. Move the term to the left side:
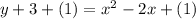
3. Simplifying and factoring:
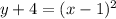
4. Solve for "y":
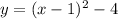
Now you can identify that:
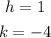
The answer is:
a. Vertex form:
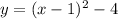
b. Vertex: