Question

Find an equation of the line tangent to the curve y=1/2(ln(sin^2(x))) at the point (pi/4 , -1/2ln2)

Answer 1

Given:

Equation of Curve is:

`y=(1)/(2)\ln (\sin ^2x)`

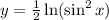
To find: Equation of tangent to the curve at point

`((\pi)/(4),(-1\ln 2)/(2))`

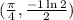
Equation of tangent to the curve is given by:

`y-y_1=m(x-x_1)`

where, m is slope of line.

Now, m is derivative of y with respect to x at given point.

Hence,

`\begin{gathered} m=(1)/(2)\text{ }*(2\sin x\cos x)/(\sin^2x) \\ m=\frac{\cos \text{ x}}{\sin \text{ x}} \\ m=\cot \text{ x} \end{gathered}`

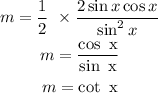
At given point, the slope m is:

`\begin{gathered} m=\cot ((\pi)/(4)) \\ m=1 \end{gathered}`

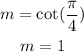
Therefore,the equation of tangent to the curve is given as:

`\begin{gathered} y-y_1=1(x-x_1) \\ y-(\frac{-1(\ln \text{ 2))}}{2})=x-(\pi)/(4) \\ \frac{2y+\ln \text{ 2}}{2}=(4x-\pi)/(4) \\ 2y+\ln 2=(4x-\pi)/(2) \end{gathered}`
`\begin{gathered} 4y+2\ln 2=4x-\pi \\ 4y=4x-\pi-2\ln 2 \end{gathered}`

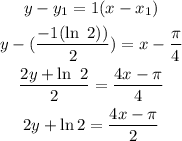
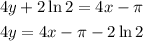
Thus the required equation of tangent to the curve is

`4y=4x-\pi-2\ln 2`