Determine the length of side AB.
![\begin{gathered} AB=\sqrt[]{(-2-2)^2+(4-1)^2} \\ =\sqrt[]{16+9} \\ =5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nsev8vni2ck1u39due2dt1n1xjsf9j2uvo.png)
Determine the length of BC.
![\begin{gathered} BC=\sqrt[]{(-1-2)^2+(-3-1)^2} \\ =\sqrt[]{9+16} \\ =5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7mf95ncqeu636pq78ayuibudvfhfuhhx2q.png)
Determine the length of CD.
![\begin{gathered} CD=\sqrt[]{(-5+1)^2+(0+3)^2} \\ =\sqrt[]{16+9} \\ =5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6zk68cl6imch80vdvcnp6kg3xgb12dlrlv.png)
Determine the length of side DA.
![\begin{gathered} DA=\sqrt[]{(-2+5)^2+(4-0)^2} \\ =\sqrt[]{9+16} \\ =5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/a4dr5jpc8l173sreh0g2md2zt3yrrxfad1.png)
All sides of quadilateral are equal. So quadilateral is a square or rhombus with side of 5 units.
Determine the length of diagonal AC and BD.
![\begin{gathered} AC=\sqrt[]{(-1+2)^2+(-3-4)^2} \\ =\sqrt[]{1+49} \\ =\sqrt[]{50} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/srlyfykula1ecbcgn3zjdh36ckk0u6uwtk.png)
![\begin{gathered} BD=\sqrt[]{(-5-2)^2+(0-1)^2} \\ =\sqrt[]{49+1} \\ =\sqrt[]{50} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8ei6k3at1rt5g0v7w2fj9s586elym6wnx9.png)
Diagonals are equal so quadilateral is a square.
Determine the area of square with side 5.
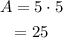
So area is 25 square units.