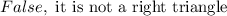Step 1
Given;

A triangle in which one of the interior angles is 90° is called a right triangle. The longest side of the right triangle, which is also the side opposite the right angle, is the hypotenuse and the two arms of the right angle are the height and the base.
For a right triangle, the sum of the square of the adjacent and the square of the opposite is equal to the square of the hypotenuse, the longest side of the triangle.
Apply the Pythagoras theorem to verify if the triangle is a right-angle triangle.
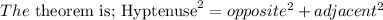
![\begin{gathered} Hypotenuse=18,\text{ the longest side} \\ opposite=16 \\ adjacent=8 \\ Note;\text{ The two other side length can be interchanged. Just make sure the hypothenus is the longest side} \end{gathered}]()
Determine if the equation holds after substitution to determine if the triangle is a right triangle.
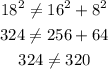
Since we do not have 324=324, the Pythagoras theorem is not obeyed and the triangle is not a right triangle.
Answer;