We know that the given triangles are similar. That means Angles Y and B are congruent. So, our job is to find Angle B first using trigonometric reasons. Let's use the tangent which is equal to the ratio between the opposite leg and the adjacent leg to angle B
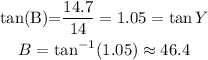
Which means angle Y is also 46.4°, approximately. Also, the tangent of Y is 1.05 too, because Y and B are congruent. Now, let's find the sine and cosine of B or Y (remember they are equal).
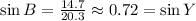
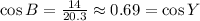
Therefore, the tanY is 1.05, sinY is 0.72 and cosY 0.69.