For this problem, we are given the value of x in the function of t, and the value of y in the function of t. We need to represent y in the function of f.
The first step is to isolate t on the x equation:
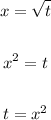
Then we need to replace the expression for t on the right side of the function for y.
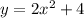
The correct answer is the third one. The interval get decreased in half, because of the relation between x and t.