Question

You and your group need to calculate the height of the triangle below to emboss a pennant. Assume that the triangle is isosceles. Assume the angle between the two identical sides is 70 degrees and that the opposite side is 3 metres. Calculate the height of the triangle to the nearest tenth of a cm.

Answer 1

To find the height of a isosceles triangle having the angle between the equal sides and the opposite side of it use the next properties:

The line that describes the height of an isosceles triangle is a bisector of angle between equal sides, and also a bisector of opposite side (different side).

Using the right triangle formed and the next trigonometric ratio find h:

`tan\theta=(opposite)/(adjacent)`
`\begin{gathered} tan((70)/(2))=(3/2)/(h) \\ \\ tan35=(1.5)/(h) \end{gathered}`

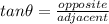
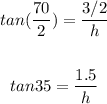
solve h:

`\begin{gathered} h*tan35=1.5 \\ h=(1.5)/(tan35) \\ \\ h=2.14m \end{gathered}`

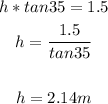
The height of the given triangle is: 2.1m (tenth of a meter)