Question

N The three side lengths of a triangle are 7, 8, and 9. Classify the triangle as an acute, obtuse, or right triangle. A Acute B Obtuse C Right triangle D None of the above

Answer 1

For this exercise you need to use the following theorems in order to classify the triangle:

1. If it is a Right triangle, then:

`c^2=a^2+b^2`

Where "c" is the hypotenuse of the Right triangle.

2. If it is an Obtuse triangle, then:

`c^2>a^2+b^2`

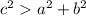
Where "c" is the longest side of the triangle.

3. If it is an Acute triangle, then:

In this case, knowing the side lengths of the triangle given in the exercise, you can identify that:

[tex]c=9" src="
`image`

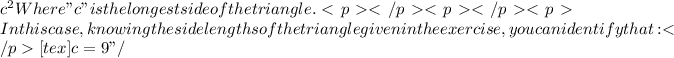
So you can classify it using the theorems, as following:

`\begin{gathered} 9^2=7^2+8^2 \\ 81\\e113 \end{gathered}`

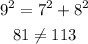
It is not a Right triangle.

`\begin{gathered} \\ 81>113\text{ }\mleft(False\mright) \end{gathered}`

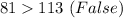
So it is not an Obtuse triangle.

`81<113\text{ }(True)`

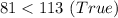
It is an Acute triangle.

The answer is: Option A.