We need to multiplicate two matrices. The first matrix is composed of the values provided in the table, that is,
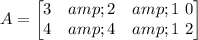
The other matrix is composed of the score of each play, that is,

Notice that the order of each score is important. They are located in the same order as matrix A, that is, TD, FG, S, and PAT.
Multiplying AxB we get:
![A\cdot B=\begin{bmatrix}{3} & {2} & {1\text{ }0} \\ {4} & 4 & 1{\text{ 2}}{}\end{bmatrix}\cdot\begin{bmatrix}{6} & {} & {} \\ {}3 & & \\ {}2 & {} & \\ 1\end{bmatrix}=\begin{bmatrix}{3\cdot6}+2\cdot3+1\cdot2+0\cdot1 & {} & {} \\ {}{4\cdot6}+4\cdot3+1\cdot2+2\cdot1 & & \\ {} & {} & \end{bmatrix}=\begin{bmatrix}26 & {} & {} \\ {}{}40 & & \\ {} & {} & \end{bmatrix}]()
Notice that to multiply two matrices, the number of columns of the first matrix
should be equal to the number of files of the second matrix
From the matrix multiplication, the score of team A was 26 points and the score of team B was 40 points.