Question

In the coordinate plane above, there is a circle with center at point (4) are A(1, -1) and B(8,6). Determine the equation of the line that goes through points A and a. b. Does this line pass through the center of the circle? Explain how yo < 10 Syllabus & Classwork Packet (3.1-3.4) ORA KE SMEN

Answer 1

toLet's begin by listing out the information given us:

`\begin{gathered} origin=(4,3) \\ A\mleft(1,-1\mright),B\mleft(8,6\mright) \end{gathered}`

For a circle, we have the radius represented by r, the origin denoted by (h,k) with coordinates being (x, y)

To determine the equation of the line that goes through points A and B, we solve thus:

`\begin{gathered} y=mx+b \\ m=(\Delta y)/(\Delta x)=(6-(-1))/(8-1)=(6+1)/(7)=(7)/(7)=1 \\ We\text{ proceed to use the point-slope formula:} \\ y-y_1=m(x-x_1) \\ y-(-1)=(x-1)\Rightarrow y+1=x-1 \\ y=x-1-1\Rightarrow y=x-2 \\ y=x-2 \\ \\ \therefore The\text{ e}quation\text{ of the is given by, }y=x-2 \end{gathered}`

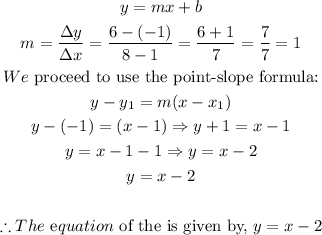
To determine if this line passes through the origin, we simply substitute the coordinate of the origin into the equation of the line:

`\begin{gathered} y=x-2 \\ (x,y)=(4,3) \\ 3=4-2\Rightarrow3\\e2 \\ 3\\e2 \\ \therefore\text{This line does not pass through the center of the circle} \end{gathered}`

Therefore, this line does not pass through the center of the circle