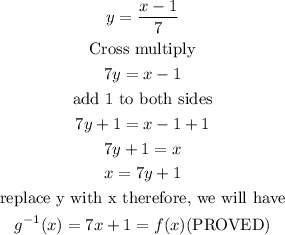Question

Verify that f and g are inverse functions algebraically. Show all your work.f(x)=7x+1 and g(x)=x-1/7

Answer 1

The functions given are

`\begin{gathered} f(x)=7x+1 \\ g(x)=(x-1)/(7) \end{gathered}`

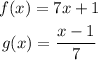
We are asked to prove that

`\begin{gathered} f^(-1)(x)=g(x) \\ g^(-1)(x)=f(x) \end{gathered}`

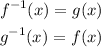
Let

`\begin{gathered} f(x)=y=7x+1 \\ y=7x+1 \end{gathered}`

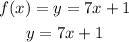
Concept: To get the inverse of a function, we will make x the subject of the formula and then replace the value of y with x

`\begin{gathered} y=7x+1 \\ \text{substract 1 from both sides} \\ y-1=7x+1-1 \\ y-1=7x \end{gathered}`

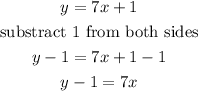
Divide both sides by 7

`\begin{gathered} 7x=y-1 \\ (7x)/(7)=(y-1)/(7) \\ x=(y-1)/(7) \\ \text{replace the value of y with x} \\ f^(-1)(x)=(x-1)/(7)=g(x)(\text{PROVED)} \end{gathered}`

Alternatively,

let

`\begin{gathered} g(x)=y=(x-1)/(7) \\ y=(x-1)/(7) \end{gathered}`

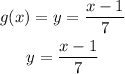
To get the inverse of a function, we will make x the subject of the formula and then replace the value of y with x

`\begin{gathered} y=(x-1)/(7) \\ \text{Cross multiply} \\ 7y=x-1 \\ \text{add 1 to both sides} \\ 7y+1=x-1+1 \\ 7y+1=x \\ x=7y+1 \\ \text{replace y with x therefore, we will have} \\ g^(-1)(x)=7x+1=f(x)(\text{PROVED)} \end{gathered}`