Let the coordinate be as follows.
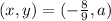
Substitute the coordinates into the equation.
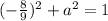
Simplify the left side of the equation.
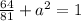
Subtract both sides of the equation by 64/81.
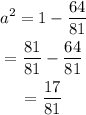
To obtain the value of a, use the square root property. Find the square root of both sides of the equation.
![a=\pm\sqrt[]{(17)/(81)}=\pm\frac{\sqrt[]{17}}{9}](https://img.qammunity.org/2023/formulas/mathematics/college/6g8794s9riwgvzqdhad9cc8ihtft3bjl8j.png)
Thus, the values of a is as follows.
![a=\frac{\sqrt[]{17}}{9}\text{and -}\frac{\sqrt[]{17}}{9}](https://img.qammunity.org/2023/formulas/mathematics/college/t85tjn14exdxaqh6ivkswtojya85tq366p.png)