Question

What is at 6% interest And what is at 14% interest

Answer 1

The rule of the simple interest is

`I=\text{PRT}`

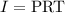
P is the initial amount

R is the rate in decimal

T is the time

Let her put $x in the account of 6%, and $y in the account of 14%

Since the amount in the 14% is more by 900, then

`y=x+900\rightarrow(1)`

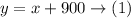
Let the first account has I1 interest and the second amount has I2 interest

`I_1=x(R_1)(1)`

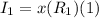
Since R1 = 6%

Change it to decimal by dividing it by 100

`R_1=(6)/(100)=0.06`

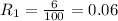
Then

`\begin{gathered} I_1=x(0.06)(1) \\ I_1=0.06x \end{gathered}`

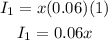
Since R2 = 14%, then

`\begin{gathered} I_2=y((14)/(100))(1) \\ I_2=0.14y \end{gathered}`

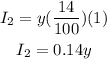
Since the total interest is $209, then add I1 and I2 and equate the sum by 209

`0.06x+0.14y=209\rightarrow(2)`

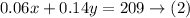
Substitute y in equation (2) by equation (1)

`0.06x+0.14(x+900)=209`

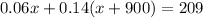
Simplify the left side

`\begin{gathered} 0.06x+0.14(x)+0.14(900)=209 \\ 0.06x+0.14x+126=209 \end{gathered}`

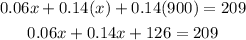
Add the like terms on the left side

`\begin{gathered} (0.06x+0.14x)+126=209 \\ 0.2x+126=209 \end{gathered}`

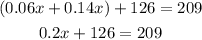
Subtract 126 from both sides, then divide the 2 sides by 0.2 to find x

`\begin{gathered} 0.2x+126-126=209-126 \\ 0.2x=83 \\ (0.2x)/(0.2)=(83)/(0.2) \\ x=415 \end{gathered}`

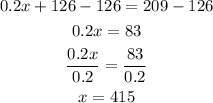
Substitute x in equation (1) by 415

`\begin{gathered} y=900+415 \\ y=1315 \end{gathered}`

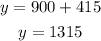
6% is $415

14% is $1315