Problem:
Solve the equation for all values of x by completing the square.
x^2 + 4x + 3 = 0
remember the following:
To solve

by completing the square, we carry out the following steps:
1. Transform the equation so that the constant term, c, is only on the right-hand side. In our case:
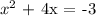
2. If a , the leading coefficient (the coefficient of the term x^2), is not equal to 1, divide both sides by a. Notice that in our case a = 1. Then, we don't do this step.
3. Add (b/2a)^2 to the right and the left side of the equation, that is:
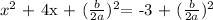
in our case note that b = 4 and a = 1, so we have:
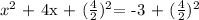
this is equivalent to say:
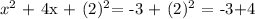
this is equivalent to say
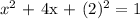
this is equivalent to say:
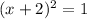
now, we take the square root of both sides of the equation
![\sqrt[]{(x+2)^2}=\sqrt[]{1}](https://img.qammunity.org/2023/formulas/mathematics/college/icplh5qrkn4pydi12gdp79zb3ipvy26to3.png)
this is equivalent to say:
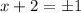
solve for x
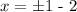
then, we have two solutions:

and

the two roots(zeros) are x = -1 and x = -3