Question

Turn object attached to a spring oscillates around the position and is represented by the function Y= 2 cos(2pi(x-0.02)),With time in x seconds. When does a height of 1 foot occur on the interval 0

Answer 1

We are given the function

`y=2\cos (2\pi(x-0.02))`

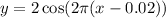
In order to find the points at which the the height of 1 foot occurs, we consider the equation

`1=2(\text{cos}(2\pi(x-0.02))`

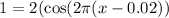
We begin working on it to solve it

`(1)/(2)=\cos (2\pi x-0.04\pi)`
`\arccos ((1)/(2))=2\pi x-0.04\pi`
`(\pi)/(3)=\pi(2x-0.04)`
`(1)/(3)=2x-0.04`
`x\approx0.19`

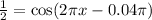
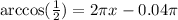
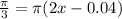
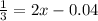
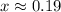
In order to find the other point in the interval 0As we can see, the other point that satisfies the equation is x=0.853.

In conclussion, a height of 1 foot occurs at 0.19 and 0.853 seconds.

Another way we can find the second value of x is by noting that

`\cos ((5\pi)/(3))=(1)/(2)`

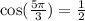
And so

`\arccos ((1)/(2))=(5\pi)/(3)`

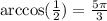
With these in mind, we go back to the equation

`(5\pi)/(3)=\pi(2x-0.04)`
`(5)/(3)=2x-0.04`

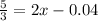
and so x=0.853