Question

Hello, I need help solving this word problem for the dimensions of a rectangle. Thank you so much !

Answer 1

Let's use the variable L to represent the length and W to represent the width.

If the length is 3 yd less than double the width, we can write the following equation:

`L=2W-3`

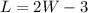
If the area is equal to 14 yd², we have this equation:

`L\cdot W=14`

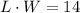
Let's use the value of L from the first equation into the second one, then we solve the resulting equation for W:

`\begin{gathered} (2W-3)\cdot W=14 \\ 2W^2-3W=14 \\ 2W^2-3W-14=0 \\ W=\frac{-(-3)\pm\sqrt[]{(-3)^2-4\cdot2\cdot(-14)}}{2\cdot2} \\ W=\frac{3\pm\sqrt[]{9+112}}{4} \\ W=(3\pm11)/(4) \\ W_1=(3+11)/(4)=(14)/(4)=3.5 \\ W_2=(3-11)/(4)=-(8)/(4)=-2 \end{gathered}`

Since a negative value for the width is not valid, we have W = 3.5 yd.

Now, calculating the length, we have:

`\begin{gathered} L=2W-3 \\ L=2\cdot3.5-3 \\ L=7-3 \\ L=4\text{ yd} \end{gathered}`

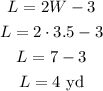
Therefore the length is 4 yards and the width is 3.5 yards.