Given the graph of the Direct Variation, you can identify this point:
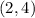
By definition, the equation of a Direct Variation has this form:
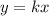
Where "k" is the Constant of Variation.
In this case, knowing the point shown before, you can set up that:
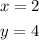
Now you can substitute these values into the equation and solve for "k":
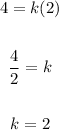
Therefore, the equation that represents the line given in the exercise is:
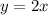
Since you need to find the value of "y" when:
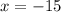
You need to substitute that x-value into the equation and evaluate:
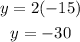
Hence, the answer is: Option A.