Question

In slope-intercept form, what is the equation of the line passing through the points (2, 13) and (5, 22)? A. y=-3x + 19B. y = 1/3x+7C.y = 3x + 7D. y = 3x - 7

Answer 1

We have to find the line that pass through this two points (2, 13) and (5, 22).

First, we can calculate the slope as:

`m=(y_2-y_1)/(x_2-x_1)=(22-13)/(5-2)=(9)/(3)=3`

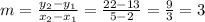
Then, we can write the slope-point form of the equation using any of the two points and the slope and rearrange:

`\begin{gathered} y-y_0=m(x-x_0) \\ y-13=3(x-2) \\ y=3x-3\cdot2+13 \\ y=3x-6+13 \\ y=3x+7 \end{gathered}`

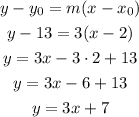
Answer: y = 3x + 7 [Option C]