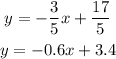Answer:
y=-0.6x+3.4
Explanation:
First, by definition, two lines are parallel if they have the same slope.
Given the equation of the line:

We find the slope by rewriting the line in the slope-intercept form:
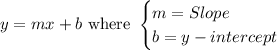
This gives:
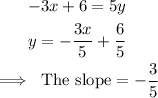
Since the two lines are to be parallel, the new line will have a slope of -3/5 and pass through the point (-4,1).
Substitute x=-4, y=1 and m=-3/5 into the slope-intercept form:
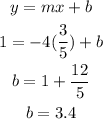
The equation of the line is: