1 Answer

Felix Ebert · Answer 1 · 2023-10-13T08:09:03+0000

Answer:

The two lines are parallel

Step-by-step explanation:

The slope-intercept form of the equation of a line is:

y = mx + c

where m represents the slope

c represents the y-intercept

If two lines have equations:

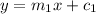
$y=m_1x+c_1_{}$
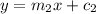
y=m_2x+c_2

The two lines are parallel if m₁ = m₂

For the line 5y +2x = 1

This can be rewritten as:

$y\text{ = -}(2)/(5)x+(1)/(5)$

The slope, m₁ = -2/5

The second line is:

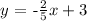
$y\text{ = -}(2)/(5)x+3$

m₂ = -2/5

Since m₁ = m₂ = -2/5, the slopes of the two lines are equal, hence the two lines are parallel

Please log in or register to add a comment.