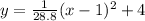Givens.
• The vertex is (1,4).
,
• The directrix is y = 16/5.
The parabola opens vertically because the directrix is a horizontal line that passes through the point (0,16/5).
But, we know that the focus point has the same distance from the vertex as the directrix, so the focus point would be F(1, 11.2). Given that the parabola opens up, the equation has the following form.
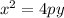
Where p = 7.2, use this value to find the equation.
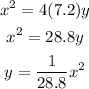
But, we still have something to add, use the vertex to find the exact equation, remember that the x-coordinate of the vertex goes with x, and the y-coordinate of the vertex goes with y.
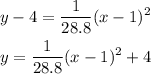
Therefore, the equation of the parabola is