Question

david invested 89000 in an account paying an intrest rate of 3.1% compounded continuously. assuming no deposits or with drawls are made how much money to the nearest ten dollars would be in the account after 15 years?

Answer 1

The information we have is:

Principal, the invested amount:

`P=89,000`

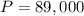
Interest rate:

`r=3.1\text{ percent }`

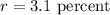
We will need the percent as a decimal, so we divide by 100:

`r=0.031`

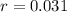
Time of the investment in years:

`t=15`

Since the investment is compounded continuously, we need to use the formula for continuous compounding:

`A=Pe^(rt)`

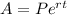
Where P, r, and t are the values we defined earlier. And A is the Amount after 15 years. Also, e is a mathematical constant:

`e=2.7183`

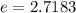
Substituting these values into the formula:

`A=(89,000)(2.7183)^((0.031*15))`

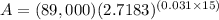
Solving the operations:

`\begin{gathered} A=(89,000)(2.7183)^((0.465)) \\ A=(89,000)(2.7183)^((0.465)) \\ A=(89,000)(1.592) \\ A=141,689.7 \end{gathered}`

Answer: $141,689.7

To round the answer to the nearest ten dollars, we should round the last three digits: 89.7 to the nearest tens which is 90.

So the rounded answer will be: $141,690