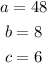Question

Use the clues to determine which number each Symbol represents

Answer 1

For each of the numbers, let us attribute a different letter for each symbol, then we will solve the system of equations.

1)

Let it be:

Box = b ; Arrow = a ; Owl = o

then, we write the following system of equations:

`\begin{gathered} b* a=o \\ o-b=45 \\ a+b=19 \end{gathered}`

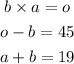
To solve the present problem, let's start with summing the second and the third equations. This will give us the sum of a and o equal to a number. Then we can isolate a and substitute in the first equation. It will allow us to determine the value of b, as follows:

2nd + 3rd equations:

`\begin{gathered} o+b+a-b=45+19 \\ o+a=64 \\ a=64-o \end{gathered}`

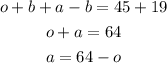
substituting in the first equation, we find:

`\begin{gathered} b*(64-o)=o \\ b=(o)/(64-o) \end{gathered}`

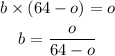
Now we can substitute it into the second equation, as follows:

`\begin{gathered} o-(o)/(64-o)=45\Rightarrow(64o-o^(2)-o)/(64-o)=45 \\ 63o-o^2=45*64-45o\Rightarrow63o-o^(2)=2880-45o \\ o^(2)-108o+2880=0 \end{gathered}`

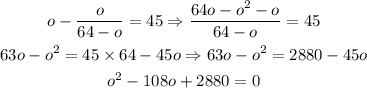
Solving the present equation by using the Bhaskara formula, we find two possible values for o:

`\begin{gathered} o_1=48 \\ o_2=60 \end{gathered}`

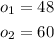
Let us solve to each possible:

For o = 48, we substitute into the first two equations and we find the following:

`\begin{gathered} b* a=48 \\ 48-b=45\Rightarrow b=3 \\ \\ \Rightarrow3* a=48\Rightarrow a=(48)/(3) \\ a=16 \end{gathered}`

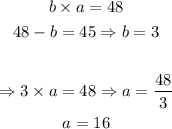
One of the possible solutions is:

`\begin{gathered} o=48 \\ a=16 \\ b=3 \end{gathered}`

The second possible solution, for o = 60, we have:

`\begin{gathered} b* a=60 \\ 60-b=45\Rightarrow b=15 \\ \\ 15* a=60\Rightarrow a=(60)/(15) \\ a=4 \end{gathered}`

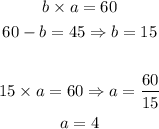
Another possible solution is the following:

`\begin{gathered} a=4 \\ b=15 \\ o=60 \end{gathered}`

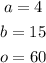
Now, let's work on the second problem:

2)

Let's set the value of: heart = h, the other unknown figure = u

`\begin{gathered} u*2=h-6 \\ h-u=23 \end{gathered}`

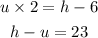
To solve it, let's isolate h in the second equation and substitute it into the first one to find the value of u.

`\begin{gathered} h=23+u \\ 2u=u+23-6 \\ \Rightarrow u=17 \end{gathered}`

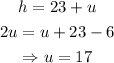
Substituting it in the second equation again, we have:

`\begin{gathered} h-17=23 \\ h=17+23=40 \\ h=40 \end{gathered}`

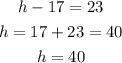
From the solution developed above, we conclude that the solution is:

`\begin{gathered} h=40 \\ u=17 \end{gathered}`

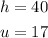
3)

For a sake of simplicity, let us call the three figures in the first relation of a, b, and c, respectively. Then we have:

`\begin{gathered} a* b=c \\ (a)/(b)=6 \\ c-a=36 \end{gathered}`

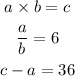
By isolating b in the second equation, and c in the third equation, and then substituting both into the first one, we have the following:

`\begin{gathered} b=(a)/(6) \\ c=a+36 \\ \\ \Rightarrow a*(a)/(6)=a+36 \\ a^2-6a-216=0 \end{gathered}`

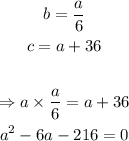
The solutions for the present equation, from the Bhaskara formula, are:

`\begin{gathered} a_1=-12 \\ a_2=18 \end{gathered}`

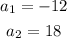
For the value a = -12, we have:

`\begin{gathered} -12b=c \\ -(12)/(b)=6\Rightarrow b=-2 \\ c-(-12)=36\Rightarrow c=24 \end{gathered}`

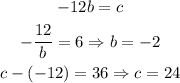
This would lead to the first solution, which is:

`\begin{gathered} a=-12 \\ b=-2 \\ c=24 \end{gathered}`

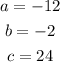
For the value a = 18, we would have:

`\begin{gathered} 18b=c \\ (18)/(b)=6\Rightarrow b=3 \\ c-18=36\Rightarrow c=54 \end{gathered}`

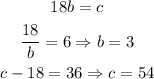
And the second possible solution for the number 3 is:

`\begin{gathered} a=18 \\ b=3 \\ c=54 \end{gathered}`

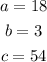
Now, let's solve number 4.

4)

Let's name the three figures as a, b, and c, respectively.

`\begin{gathered} (a)/(b)=c \\ c* a=288 \\ a-b=40 \end{gathered}`

The first step is to isolate c in the second equation and b in the third, substitute in the first equation, then we will find the value of a.

`\begin{gathered} c=(288)/(a) \\ b=a-40 \\ \\ (a)/(a-40)=(288)/(a)\Rightarrow a^(2)=288a-11,520 \\ a^(2)-288a+11,520=0 \end{gathered}`

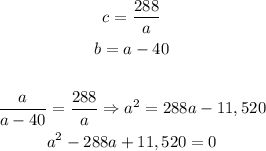
The values which are the solution for this equation, from the Bhaskara equation, are:

`\begin{gathered} a_1=240 \\ a_2=48 \end{gathered}`

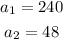
Using the value a = 240, we find the following values:

`\begin{gathered} (240)/(b)=c \\ 240c=288\Rightarrow c=1.2 \\ 240-b=40\Rightarrow b=200 \end{gathered}`

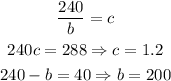
From this value of a, the solution is:

`\begin{gathered} a=240 \\ b=200 \\ c=1.2 \end{gathered}`

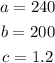
For the second value of a, a = 48, we have:

`\begin{gathered} (48)/(b)=c \\ c*48=288\Rightarrow c=6 \\ 48-b=40\Rightarrow b=8 \end{gathered}`

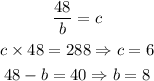
From this, the last solution for the number 4 is:

`\begin{gathered} a=48 \\ b=8 \\ c=6 \end{gathered}`