The regression model of profit versus year since 2014 gives us the following equation:
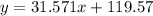
We have to estimate in which year the profits is expected to be 404 thousand dollars.
We can do it by replacing y with 404 and solve for x:
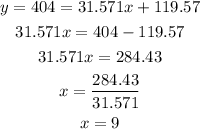
As x represents the number of years since 2014, the calendar year is 2014+9 = 2023.
Answer:
Equation: y=31.571x+119.57
Year: 2023