Step-by-step explanation
We are asked to resolve a conditional probability question
For the given question, we will have to find the probability of obtaining a green marble given not yellow
We have the box containing one green marble, two yellow marbles, and six pink marbles
Green = 1
Yellow = 2
Pink = 6
Probability is the ratio of the number of possible outcomes to the total outcomes
we will apply the formula
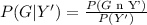
Where
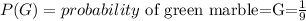

Thus
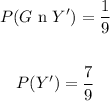
Therefore, we will have the answer as
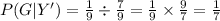
Therefore, the answer will be
