Solution:
Let the price of mango, strawberry and chocolate flavors be x, y, and z respectively.
Thus,
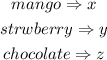
From the table below:
Given that the total sales in shift 1 is $419, $649 in shift 2, and $96 in shift 3, this implies that
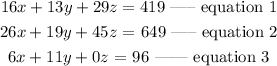
From the above system of equations, we can resolve into matrices of the form:
This gives:
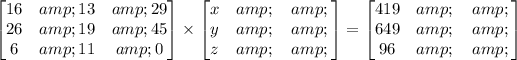
Where:
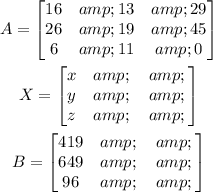
To solve for the unknowns, we use the Cramer's rule expressed s
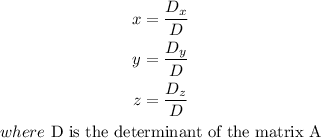
To evaluate the price of one chocolate, which is z, we have

Hence, the price of one chocolate is
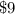
The correct option is D