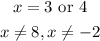Answer::
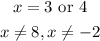
Step-by-step explanation:
Given the rational function:
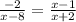
Step 1: Cross-multiply
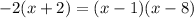
Step 2: Expand and simplify
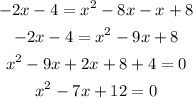
Step 3: Solve the quadratic equation for x.
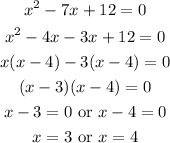
Step 4: Find the excluded values
The excluded values are the values at which the function is undefined.
Set the denominators equal to zero.
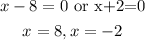
Thus the solution of the function is: