Question

Fill in the missing spaces in the table below.g(x)= 3x² +6x-4(0, -4)--7)Featuresf(x)= - - 2x² ++ 8x + 1y-interceptvertex(2,axis ofx= 2symmetrymaximum orminimum valueopens upwardor downwardminimumupwardFeaturesy-interceptvertexf(x) = - 2x + 8x+1(0,1)g(x)= 3x² +6x-4(0,- 4)0.-7)(Type an ordered pair.)(Simplify your answer.)

Answer 1

Part A

Given f(x) defined below:

`f(x)=-2x^2+8x+1`

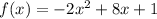
The y-intercept is the value of y when x=0.

`\begin{gathered} f(0)=-2(0)^2+8(0)+1=1 \\ y-\text{intercept:}(0,1) \end{gathered}`

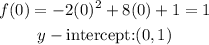
Vertex

Since the axis of symmetry is given as x=2:

`\begin{gathered} f(2)=-2(2)^2+8(2)+1 \\ =-2(4)+16+1 \\ =9 \\ \implies\text{Vertex:}(2,9) \end{gathered}`

Minimum/Maximum Value

Since the coefficient of x² is negative, there is a maximum value.

• Maximum Value = 9

,

• The graph opens downwards.

Part B

Given g(x) defined below:

`g(x)=3x^2+6x-4`

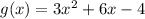
The axis of symmetry is derived using the formula below:

`\begin{gathered} x=-(b)/(2a),a=3,b=6 \\ x=-(6)/(2*3)=-(6)/(6) \\ x=-1 \end{gathered}`

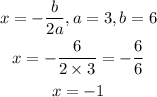
• Axis of Symmetry: x=-1

,

• Vertex: (-1,-7)