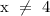Restricted values are values that will make the denominator equal to 0.
The denominator in the given expression is:
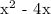
Now, let's determine what values should be restricted for the denominator not to be zero.
We get,
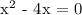
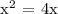
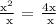
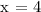
Therefore, the restricted value of the given ratio is 4.
Or,