The future value of the investment when interest is compounded
(a) annually; A = $3,408.29
(b) monthly; A = $3,427.30
(c) daily; A = $3,429.02
(d) continuously; A = $3,429.08
e) the doubling time T; t = 17.54803 years
What is the future value?
P = $2500,
r=3.95% = 0.0395
t = 8 yr
A. Annually
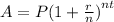
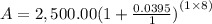
A = 2,500.00(1 + 0.0395)⁸
A = 2,500.00(1.0395)⁸
A = $3,408.29
B. Monthly
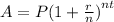
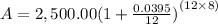
A = 2,500.00(1 + 0.0032916666666667)⁹⁶
A = 2,500.00(1.0032916666667)⁹⁶
A = $3,427.30
C. Daily
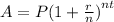
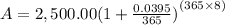
A = 2,500.00(1 + 0.00010821917808219)²⁹²⁰
A = 2,500.00(1.0001082191781)²⁹²⁰
A = $3,429.02
D. Continuously
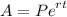
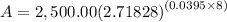
A = $3,429.08
E.
Doubling time, t when A = 2P
= 2(2,500)
= $5,000.00
t = ln(A/P) / r
t = ln(5,000.00/2,500.00) / 0.0395
t = 17.54803 years