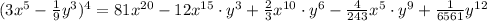Part (a).
Sigma notation (or summation notation) of binomial expansion is the following:
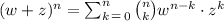
where
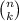
denotes the binomial coefficient.
In our case, n is 4 and
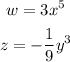
So by substituting these terms into the sigma expantion, we have
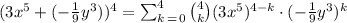
So, the sum in summation notation is:
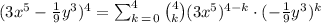
Part b.
By expanding the above sum, we have
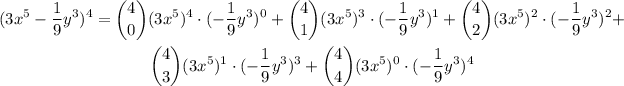
Since
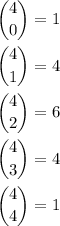
we have
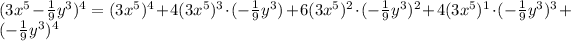
which gives
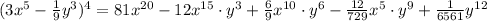
Therefore, the simplified expansion is given by: