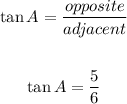Question

Given sin A=-5/and that angle Ais in Quadrant III, find the exact value oftan Ain simplest radical form using a rational denominator.

Answer 1

Given:

`\sin A=-\frac{5}{\sqrt[]{61}}`

the angle A is in QIII, So, the value of the tan A will be positive

To find tan A, we need to find the third side of the right-angle triangle that angle A fall inside it

From the sin A = opposite/hypotenuse

opposite side = 5

hypotenuse = √61

the adjacent side will be calculated using the Pythagorean theorem

`adjacent=\sqrt[]{(\sqrt[]{61})^2-5^2}=\sqrt[]{61-25}=\sqrt[]{36}=6`

The value of tan A will be as follows:

`\begin{gathered} \tan A=(opposite)/(adjacent) \\ \\ \tan A=(5)/(6) \end{gathered}`