We need to find two numbers that meet the following...
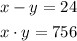
first, let's clear x from the first equation

Second, substitute the solutions x = 24 + y into xy = 756
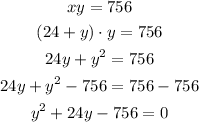
Now, we need to solve this second grade equation
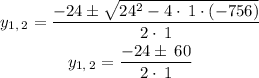
We will obtain two values for y

We will only use the positive value
Now, we just have to replace y=18 into x=24+y
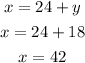
In conclusion, the two positive numbers that meet the conditions are:
18 and 42