The surface area is the sum of the area of the square plus the area of the 4 equal triangles. So, we need to find the area of one triangle multiply by 4 and add the area of the square.
Then, the area of one triangle is
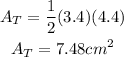
and the area of the square is
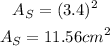
Then, the surface S is
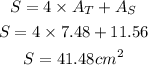
And the answer is 41.48 centimeters squared.