Question

The mean value of land and buildings per acre from a sample of farms is $1500, with a standard deviation of $300. The data set has a bell-shaped distribution. Assume the number of farms in the sample is 80. 7 ar (a) Use the empirical rule to estimate the number of farms whose land and building values per acre are between $900 and $2100.

Answer 1

Data:

Mean: $1500

Standard deviation: $300

Sample: 80.7

Empirical rule define the following intervals:

68.27% of the data are in: [μ - s, μ + s]

95.45% of the data are in: [µ – 2s, µ + 2s]

99.73% of the data are in: [µ – 3s, µ + 3s]

Being μ the mean and s the standard deviation:

You need to find the number of farms between $900 and $2100 per acre:

µ=1500

s=300

68.27% of the data will be in the interval:

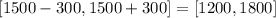
`\lbrack1500-300,1500+300\rbrack=\lbrack1200,1800\rbrack`95.45% of the data will be in the interval: [900,2100]
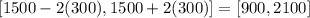
`\lbrack1500-2(300),1500+2(300)\rbrack=\lbrack900,2100\rbrack`As the 100% of the sample is 80.7, the 95.45% is: 77.02 farms
`80.7\cdot(95.45)/(100)=77.02`

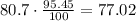
Then, the number of farms whose land and building values per acre are between $900 and $2100 is 77.02.