Question

Given: D is the midpoint of CE prove : DR = 1/2CE Reason bank simply Transitive property Division property Addition property Given Definition of midpoint Segment Addition postulate

Answer 1

Statement1: Given a line segment

`CE`

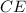
Statement 2: Definition of Midpoint

D as the midpoint

Then we have

Statement 3: Segment addition postulate

`\begin{gathered} CD+DE=CE \\ \text{ } \end{gathered}`

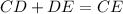
Statement 4: simplify

`CE=DE`

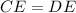
Statement 5: Addition property

Then Adding DE to both sides

`\begin{gathered} CD+DE=DE+DE \\ CD+DE=2DE \end{gathered}`

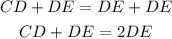
Then from the diagram,

`CD+DE=CE`

We have

Statement 6: Transitive property

`\begin{gathered} CE=CD+DE=2DE \\ \text{then } \\ CE=2DE \end{gathered}`

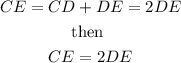
statement 7: Division property

Divide both sides by 2

`\begin{gathered} (CE)/(2)=(2DE)/(2) \\ \\ DE=(1)/(2)CE \end{gathered}`

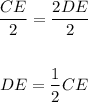
Therefore

DE=1/2 CE implies D is the midpoint of CE

Statement 1= Given

Statement2=Difine a midpoint

Statement 3=Segment addition postulate

statement 4=simplify

Statement5= Addition property

Statement 6=transitive property

Statement 7=Division property