Question

use the following question to answer the question below (the one in the picture)is a hyperbola horizontal or vertical and how can you tellwhat's the equation in general formwhat is the co verticalswhat is the foci

Answer 1

We are given the following equation of a hyperbola:

`((y+2)^2)/(4)-((x-7)^2)/(16)=1`

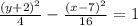
We are asked if the hyperbola is horizontal or vertical. A hyperbola is horizontal if the minus sign is next to the fraction where the y-variable is, and it is vertical if the minus sign is next to the fraction where the x-variables is, this can be expressed like this:

Horizontal Hyperbola:

`((x-h)^2)/(a^2)-\frac{(y-k)^{2^{}}}{b^2}=1`

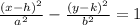
Vertical Hyperbola:

`((y-k)^2)/(b^2)-((x-h)^2)/(a^2)=1`

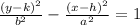
Therefore, the given hyperbola is Vertical.

Now we are asked to find the general form of the equation of the given hyperbola, to do that we need to expand the numerators, like this:

we use the following relation:

`(a+b)^2=a^2+2ab+b^2`

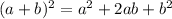
applying that we get:

`(y^2+4y+4)/(4)-(x^2-14x+49)/(16)=1`

Now we multiply both sides by 4:

`y^2+4y+4-(4)/(16)(x^2-14x+49)=4`

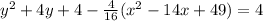
Simplifying:

`y^2+4y+4-(1)/(4)(x^2-14x+49)=4`

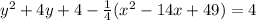
Multiplying both sides by 4

`4y^2+16y+14-x^2-14x+49=16`

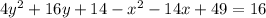
Adding like terms:

`4y^2+16y-x^2-14x+63=16`

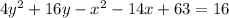
subtracting 63

`4y^2+16y-x^2-14x=-47`

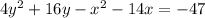
This is the general form of the given equation.

Now we are asked to find the co-vertices of the hyperbola, to do that let's remember that the coordinates of the co-vertices are given by:

`co-vertices=(h\pm b,k)`

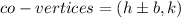
where

`\begin{gathered} h=7 \\ b=4 \\ k=-2 \end{gathered}`

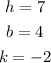
Replacing we get;

`\begin{gathered} \text{cov}1=(7+4,-2) \\ \text{cov}1=(11,-2) \end{gathered}`
`\begin{gathered} \text{cov}2=(7-4,-2) \\ \text{cov}2=(3,-2) \end{gathered}`

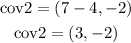
where cov1 and cov2, are co-vertex 1 and 2 respectively.

Now we are asked to find the foci, to do that let's remember that he coordinates of the foci are given by:

`\text{foci}=(h,k\pm c)`

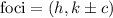
Where c is given by:

`c=\sqrt[]{a^2+b^2}`

replacing the values for a and b, we get:

`c=\sqrt[]{4+16}=\sqrt[]{20}`

Now we can replace in the equation for the foci:

`\text{foci}1=(7,-2+\sqrt[]{20})`
`\text{foci}2=(7,-2-\sqrt[]{20})`