Question

car enthusiast learns that a particular model of car, which costs $39,300 new, loses 25% of its value every year. How much will the car be worth in 9 years?If necessary, round your answer to the nearest cent.

Answer 1

Given:

The cost of the car = $ 39300.

The loss percentage =25 %.

The number of years =9 years.

The given statement is the model of the exponential decay function.

Let C be the cost of the car after t years.

The equation for the given model is

`C=a(1-r)^t`

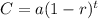
where a is the initial value and r is the rate percentage of decay.

Substitute a=39300, r=25% =0.25 and t=9 in the equation, we get

`C=39300(1-0.25)^9`
`C=39300*0.075`
`C=2947.50`

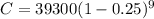
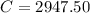
Hence the worth of the car of 9 years is $2947.50.