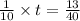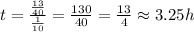Question

Bill can repair a transmission in 8 hours. It takes Henry 10 hours to do the same job. If they begin the job together and then Bill leaves after 3 hours, how long will it take Henry to finish?

Answer 1

Answer: Henry will take 3.25 hours to finish the work alone.

Step-by-step explanation

Given

• Bill can repair a transmission in 8 hours.

,

• It takes Henry 10 hours to do the same job.

,

• If they begin the job together and then Bill leaves after 3 hours, how long will it take Henry to finish?​

Procedure

Bill does 1/8 of the job per hour, while Henry does 1/10 of the work per hour. They work together 3 hours. If we assume their works are additive (no interference from one another), and considering that:

`rate* time=\text{work done}`

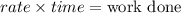
Then we can build the following relation:

`((1)/(8)+(1)/(10))*3=\text{ work done}`

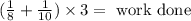
Simplifying:

`\text{ work done}=((5+4)/(40))*3=((9)/(40))*3=(27)/(40)`

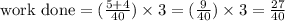
The job at the 3 hours will be 27/40 done. Then, Henry has to finish the rest of the work, which is:

`(40)/(40)-(27)/(40)=(13)/(40)`

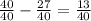
Finally, to calculate the time it will take Henry to do the job, we have to do the following:

`(1)/(10)* t=(13)/(40)`
`t=((13)/(40))/((1)/(10))=(130)/(40)=(13)/(4)\approx3.25h`