Question

In the diagram below, quadrilateral NOPQ is inscribed in circle R. Find themeasure of ZP.N70°o94RQ

Answer 1

P = 110 degrees

Step-by-step explanation:

We were given the following information:

A quadrilateral NOPQ is inscribed in a circle. This makes the quadrilateral a cyclic quadrilateral

`\begin{gathered} \angle N=70^(\circ) \\ \angle O=94^(\circ) \end{gathered}`

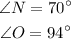
Angle P is supplementary to Angle N; both angles P & N sum up to 180 degrees:

`\begin{gathered} \angle P+\angle N=180^(\circ) \\ \angle N=70^(\circ) \\ \angle P+70^(\circ)=180^(\circ) \\ \text{Subtract ''}70^(\circ)\text{'' from both sides, we have:} \\ \angle P=(180-70)^(\circ) \\ \angle P=110^(\circ) \\ \\ \therefore\angle P=110^(\circ) \end{gathered}`

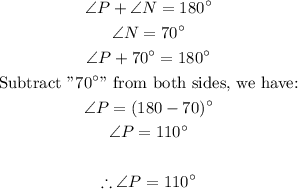
Therefore, the angle at P equals 110 degrees