Answer: B
The correct second step for the given proof is;
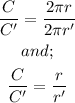
by the division property of equality.
Step-by-step explanation:
We want to find the correct second step for the given proof.
Recall that from division property of equality, when we have;
a=b and c=d, dividing the equations by each other, the equation will still be equal;
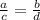
For the given Prove;
statement 1 states that the circumference circle 1 and 2 can be expressed as;
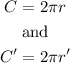
So, for step 2;
Applying the division property of equality, we have;
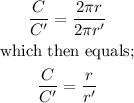
Therefore, the correct second step for the given proof is;
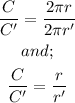
by the division property of equality.