Question

MatnYou are dealt one card from a 52 card deck. Find the probability that you are dealt a ten or a black card.The probability is I (Type an integer or a fraction. Simplify your answer.)re

Answer 1

We have to find the probability that you are dealt a ten or a black card.

Out of the 52 card deck, there are 26 black cards.

There are also 4 cards that are tens, but there are 2 cards that are both black and tens.

Then, if we define B: the event of a black card and T: the event of a ten, we can calculate the probability of B or T as:

`P(B\cup T)=P(B)+P(T)-P(B\cap T)`

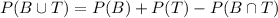
Replacing with the values of the probability (success events divided by the total possible events), we can solve this as:

`\begin{gathered} P(B\cup T)=P(B)+P(T)-P(B\cap T) \\ P(B\cup T)=(21)/(52)+(4)/(52)-(2)/(52) \\ P(B\cup T)=(21+4-2)/(52) \\ P(B\cup T)=(23)/(52) \end{gathered}`

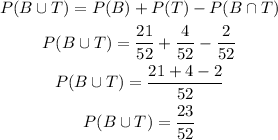
Answer: the probability of getting a black or a ten is 23/52.