ANSWER
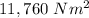
Step-by-step explanation
To find the pressure of the kerosene at the tap, we have to apply the relationship between pressure and density:
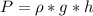
where ρ = density
g = acceleration due to gravity = 9.8 m/s^2
h = height
Therefore, the pressure of the kerosene at the tap is:
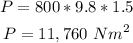
That is the answer.