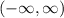Given
The equations are given
x(t)=t+5, y(t)=3t^2−4, where t is on the interval [−4,0].
Step-by-step explanation
To find the rectangular form of parametric equations
Substitute the value of t from x in y.
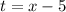
Then ,
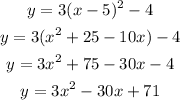
Answer
The rectangular form of parametric equations is
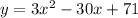
The interval where x fall is