Answer:
A
Step-by-step explanation:
To determine which sequence of transformation will map figure K onto figure K', we test each of the options using the point (6,5) in Figure K.
Option A
Reflection across x=4, 180° rotation about the origin, and a translation of (x+8,y)
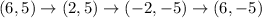
Option B
Reflection across x=4, 180° rotation about the origin, and a translation of (x-8, y)
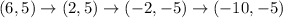
Option C
Reflection across y=4, 180° rotation about the origin, and a translation of (x+8,y)
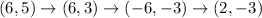
Option D
Reflection across y=4, 180° rotation about the origin, and a translation of (x-8,y)
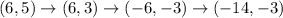
We can see that Option A is the one which maps point (6,5) to (6,-5).
Therefore, it is the sequence of transformations will map figure K onto figure K'.