Question

Given Rectangle MNPQ, what is the length of MQ? (Hint: Draw a perpendicular bisector & use Pythagorean Theorem. Round your answer to the nearest tenth!)

Answer 1

In order to find the length of MQ, we can first draw a segment from the intersection point of the diagonals (let's call it D) and parallel to sides NM and PQ, going down to point K, like this:

The segment DK has a length of half the length of PQ, so we have DK = 2.

Now, we can use the Pythagorean Theorem to find the length of KQ:

`\begin{gathered} DQ^2=DK^2+KQ^2 \\ 5^2=2^2+KQ^2 \\ 25=4+KQ^2^{} \\ KQ^2=25-4 \\ KQ^2=21 \\ KQ=4.58 \end{gathered}`

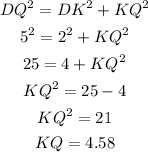
The length of KQ is half the length of MQ, so we have:

`\begin{gathered} KQ=(MQ)/(2) \\ MQ=2\cdot KQ \\ MQ=2\cdot4.58 \\ MQ=9.16 \end{gathered}`

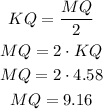
Rounding to the nearest tenth, we have MQ = 9.2 units