Question

My ex represented in the public will buy for an object and P represent the object unit three suppose that the universe

Answer 1

we have the linear equation

`p=(-(1)/(5))x+200`

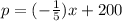
Part A

the Revenue is equal to

R(x)=p*x

substitute

`R(x)=\lbrack(-(1)/(5))x+200\rbrack\cdot x`
`R(x)=-(1)/(5)x^2+200x`

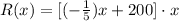
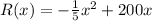
Part B

the function of revenue is a quadratic equation (vertical parabola opens downward)

the vertex represents a maximum

using a graphing tool

see the attached figure

the vertex is the point (500, 50000)

therefore

the value of x that maximizes the revenue is

x=500

Part C

For x=500

Find out the unit price

`\begin{gathered} p=(-(1)/(5))(500)+200 \\ p=100 \end{gathered}`

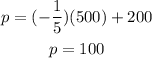
the unit price is p=$100

Part D

the maximum revenue is the y-coordinate of the vertex

the vertex is (500, 50,000)

therefore

the maximum revenue is $50,000