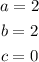Question

5 -x - 4y + 5z = -21 13) -3a - b - 3c = -8 -5a + 3b + 6c = -4 -6a - 4b +c= -20 14) -5x + 3y + 6z=4 -3x + y + 5z = -5 -4x +2y+z=17

Answer 1

To solve the system of equations:

`\begin{gathered} -3a-b-3c=-8 \\ -5a+3b+6c=-4 \\ -6a-4b+c=-20 \end{gathered}`

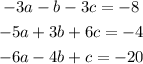
by elimination we choose two equations and eliminate one of the variables. Choosing the first two equations and multiplying the first one by 2 we have:

`\begin{gathered} -6a-2b-6c=-16 \\ -5a+3b+6c=-4 \end{gathered}`

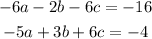
if we add the equation we get:

`-11a+b=-20`

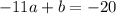
Now, from the original system we choose the second and third equations and multyply the third by -6, then we have:

`\begin{gathered} -5a+3b+6c=-4 \\ 36a+24b-6c=120 \end{gathered}`

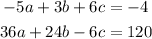
Adding the two equations we have:

`31a+27b=116`

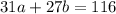
Now that we eliminate the same variable from two sets of equations we have the new system:

`\begin{gathered} -11a+b=-20 \\ 31a+27b=116 \end{gathered}`

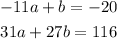
To solve this sytem we mutiply the first equation by -27, then we have:

`\begin{gathered} 297a-27b=540 \\ 31a+27b=116 \end{gathered}`

adding this equation we have:

`\begin{gathered} 328a=656 \\ a=(656)/(328) \\ a=2 \end{gathered}`

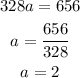
Once we have the value of a we plug it in the equation

`-11a+b=-20`

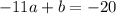
to find b:

`\begin{gathered} -11(2)+b=-20 \\ -22+b=-20 \\ b=22-20 \\ b=2 \end{gathered}`

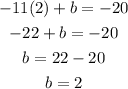
Now that we have the values of a and b we plug them in the equation

`-3a-b-3c=-8`

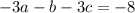
to find c:

`\begin{gathered} -3(2)-2-3c=-8 \\ -6-2-3c=-8 \\ -8-3c=-8 \\ 3c=-8+8 \\ 3c=0 \\ c=(0)/(3) \\ c=0 \end{gathered}`

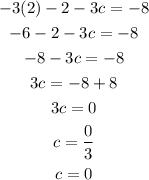
Therefore the solution of the system is:

`\begin{gathered} a=2 \\ b=2 \\ c=0 \end{gathered}`