To solve the exercise, we can first find the length of each segment using the formula for the distance between two points:
![\begin{gathered} D=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \text{ Where }(x_1,y_1)\text{ and }(x_2,y_2)\text{ are the coordinates of the points} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4ssb0v8n52q4qnlwxcryrh6nq8ozoec0lv.png)
First segment:
![\begin{gathered} (x_1,y_1)=(0,8) \\ (x_2,y_2)=\mleft(-6,0\mright) \\ D=\sqrt[]{(-6_{}-0)^2+(0-8)^2} \\ D=\sqrt[]{(-6)^2+(8)^2} \\ D=\sqrt[]{36+64} \\ D=\sqrt[]{100} \\ D=10 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9kr5r8v3phyckrlqcmdg1bovt0k3f2sc7x.png)
Second segment:
![\begin{gathered} (x_1,y_1)=\mleft(0,6\mright) \\ (x_2,y_2)=\mleft(-4.5,0\mright) \\ D=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ D=\sqrt[]{(-4.5-0)^2+(0-6)^2} \\ D=\sqrt[]{(-4.5)^2+(-6)^2} \\ D=\sqrt[]{20.25+36} \\ D=\sqrt[]{56.25} \\ D=7.5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/pkmd0vxpk2bvm1n98u2n19l9jkgkdz5iqw.png)
Now, we apply the following formula:
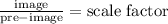
Then, we have:

Therefore, the scale factor of the dilation is 3/4.